Ensembling, Bagging, Boosting, Tree-based Models

1.Ensemble

• In statistics and machine learning, ensemble methods use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone

• Ensemble methods is a machine learning technique that combines several base models in order to produce one optimal predictive model

1.1.Why do we need to know about Ensemble Learning?

Ensemble learning is one of the most effective ways to build an efficient machine learning model. You can build an ensemble machine learning model using simple models and yet get great scores which are at par with the resource-hungry models like neural networks.

1.2.What are the different types of Ensemble Learning techniques?

There are simple and advanced ensemble learning techniques.

1. Simple:

   1. Max Voting

   2. Averaging

   3. Weighted Averaging

2. Advanced

   1. Stacking

   2. Blending

   3. Bagging

   4. Boosting

2.Bootstrapping

Bootstrapping is a sampling technique in which we create subsets of observations from the original dataset, with replacement. The size of the subsets is the same as the size of the original set.

The Bootstrap -

widely applicable and extremely powerful statistical tool bootstrap that can be used to quantify the uncertainty associated with a given estimator or statistical learning method

3. Bagging (or Bootstrap Aggregating)

Technique uses these subsets (bags) to get a fair idea of the distribution (complete set). The size of subsets created for bagging may be less than the original set.

Bagging stands for bootstrap aggregation. One way to reduce the variance of an estimate is to average together multiple estimates.

• Bootstrap Aggregation (or Bagging for short), is a simple and very powerful ensemble method. Bagging is the application of the Bootstrap procedure to a high-variance machine learning algorithm, typically decision trees.

• Suppose there are N observations and M features. A sample from observation is selected randomly with replacement(Bootstrapping).

• A subset of features are selected to create a model with sample of observations and subset of features.

• Feature from the subset is selected which gives the best split on the training data.(Visit my blog on Decision Tree to know more of best split)

• This is repeated to create many models and every model is trained in parallel

• Prediction is given based on the aggregation of predictions from all the models.

When bagging with decision trees, we are less concerned about individual trees overfitting the training data. For this reason and for efficiency, the individual decision trees are grown deep (e.g. few training samples at each leaf-node of the tree) and the trees are not pruned. These trees will have both high variance and low bias. These are important characterize of sub-models when combining predictions using bagging. The only parameters when bagging decision trees is the number of samples and hence the number of trees to include. This can be chosen by increasing the number of trees on run after run until the accuracy begins to stop showing improvement

Bagging

The idea behind bagging is combining the results of multiple models (for instance, all decision trees) to get a generalized result. Here’s a question: If you create all the models on the same set of data and combine it, will it be useful? There is a high chance that these models will give the same result since they are getting the same input. So how can we solve this problem? One of the techniques is bootstrapping.

Bootstrapping is a sampling technique in which we create subsets of observations from the original dataset, with replacement. The size of the subsets is the same as the size of the original set.

Bagging (or Bootstrap Aggregating) technique uses these subsets (bags) to get a fair idea of the distribution (complete set). The size of subsets created for bagging may be less than the original set.

1. Multiple subsets are created from the original dataset, selecting observations with replacement.

2. A base model (weak model) is created on each of these subsets.

3. The models run in parallel and are independent of each other.

4. The final predictions are determined by combining the predictions from all the models.

3.1.What is the intuition behind Bagging?

The idea behind bagging is combining the results of multiple models (for instance, all decision trees) to get a generalized result. Bagging (or Bootstrap Aggregating) technique uses subsets (bags) to get a fair idea of the distribution (complete set).

4.Boosting

Is a sequential process, where each subsequent model attempts to correct the errors of the previous model.

Boosting refers to a group of algorithms that utilize weighted averages to make weak learners into stronger learners. Unlike bagging that had each model run independently and then aggregate the outputs at the end without preference to any model. Boosting is all about “teamwork”. Each model that runs, dictates what features the next model will focus on.

Boosting

Before we go further, here’s another question for you: If a data point is incorrectly predicted by the first model, and then the next (probably all models), will combining the predictions provide better results? Such situations are taken care of by boosting.

Boosting is a sequential process, where each subsequent model attempts to correct the errors of the previous model. The succeeding models are dependent on the previous model. Let’s understand the way boosting works in the below steps.

1. A subset is created from the original dataset.

2. Initially, all data points are given equal weights.

3. A base model is created on this subset.

4. This model is used to make predictions on the whole dataset.
5. Errors are calculated using the actual values and predicted values.

6. The observations which are incorrectly predicted, are given higher weights. (Here, the three misclassified blue-plus points will be given higher weights)

7. Another model is created and predictions are made on the dataset. (This model tries to correct the errors from the previous model)
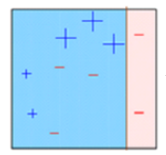
8. Similarly, multiple models are created, each correcting the errors of the previous model.

9. The final model (strong learner) is the weighted mean of all the models (weak learners).

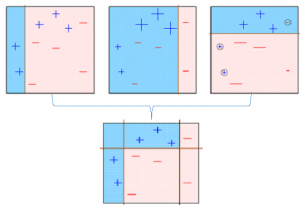
Thus, the boosting algorithm combines a number of weak learners to form a strong learner. The individual models would not perform well on the entire dataset, but they work well for some part of the dataset. Thus, each model actually boosts the performance of the ensemble.

5. Does ensemble learning improve my machine learning model?

In a word, yes! And that too drastically! Ensemble learn can improve the results of your machine learning even exponentially at times. There are two major benefits of Ensemble models:

• More accurate predictions(closer to the actual value)

• Combining multiple simple models to make a strong model improves the stability of the overall machine learning model.

What is the difference between Bagging and Boosting?

While both bagging and boosting involve creating subsets, bagging makes these subsets randomly, while boosting prioritizes misclassified subsets. Additionally, at the final step in bagging, the weighted average is used, while boosting uses majority weighted voting.

Advanced Ensemble Techniques

• Stacking

• Blending

• Bagging

• Boosting

Stacking

Stacking is an ensemble learning technique that uses predictions from multiple models (for example decision tree, knn or svm) to build a new model. This model is used for making predictions on the test set. Below is a step-wise explanation for a simple stacked ensemble:

1. The train set is split into 10 parts.
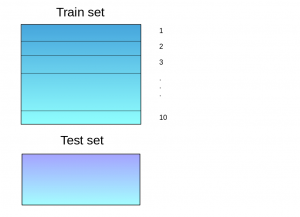
2. A base model (suppose a decision tree) is fitted on 9 parts and predictions are made for the 10th part. This is done for each part of the train set.
3. The base model (in this case, decision tree) is then fitted on the whole train dataset.

4. Using this model, predictions are made on the test set.
5. Steps 2 to 4 are repeated for another base model (say knn) resulting in another set of predictions for the train set and test set.
6. The predictions from the train set are used as features to build a new model.
7. This model is used to make final predictions on the test prediction set.

Sample code:

We first define a function to make predictions on n-folds of train and test dataset. This function returns the predictions for train and test for each model.

def Stacking(model,train,y,test,n_fold):
   folds=StratifiedKFold(n_splits=n_fold,random_state=1)
   test_pred=np.empty((test.shape[0],1),float)
   train_pred=np.empty((0,1),float)
   for train_indices,val_indices in folds.split(train,y.values):
      x_train,x_val=train.iloc[train_indices],train.iloc[val_indices]
      y_train,y_val=y.iloc[train_indices],y.iloc[val_indices]

      model.fit(X=x_train,y=y_train)
      train_pred=np.append(train_pred,model.predict(x_val))
      test_pred=np.append(test_pred,model.predict(test))
    return test_pred.reshape(-1,1),train_pred

Now we’ll create two base models – decision tree and knn.

model1 = tree.DecisionTreeClassifier(random_state=1)

test_pred1 ,train_pred1=Stacking(model=model1,n_fold=10, train=x_train,test=x_test,y=y_train)

train_pred1=pd.DataFrame(train_pred1)
test_pred1=pd.DataFrame(test_pred1)

model2 = KNeighborsClassifier()

test_pred2 ,train_pred2=Stacking(model=model2,n_fold=10,train=x_train,test=x_test,y=y_train)

train_pred2=pd.DataFrame(train_pred2)
test_pred2=pd.DataFrame(test_pred2)

Create a third model, logistic regression, on the predictions of the decision tree and knn models.

df = pd.concat([train_pred1, train_pred2], axis=1)
df_test = pd.concat([test_pred1, test_pred2], axis=1)

model = LogisticRegression(random_state=1)
model.fit(df,y_train)
model.score(df_test, y_test)

In order to simplify the above explanation, the stacking model we have created has only two levels. The decision tree and knn models are built at level zero, while a logistic regression model is built at level one. Feel free to create multiple levels in a stacking model.

Blending

Blending follows the same approach as stacking but uses only a holdout (validation) set from the train set to make predictions. In other words, unlike stacking, the predictions are made on the holdout set only. The holdout set and the predictions are used to build a model which is run on the test set. Here is a detailed explanation of the blending process:

1. The train set is split into training and validation sets.
2. Model(s) are fitted on the training set.

3. The predictions are made on the validation set and the test set.
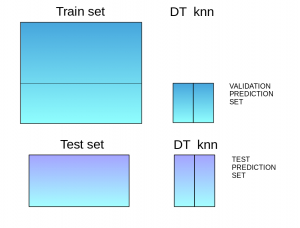
4. The validation set and its predictions are used as features to build a new model.

5. This model is used to make final predictions on the test and meta-features.

Sample Code:

We’ll build two models, decision tree and knn, on the train set in order to make predictions on the validation set.

model1 = tree.DecisionTreeClassifier()
model1.fit(x_train, y_train)
val_pred1=model1.predict(x_val)
test_pred1=model1.predict(x_test)
val_pred1=pd.DataFrame(val_pred1)
test_pred1=pd.DataFrame(test_pred1)

model2 = KNeighborsClassifier()
model2.fit(x_train,y_train)
val_pred2=model2.predict(x_val)
test_pred2=model2.predict(x_test)
val_pred2=pd.DataFrame(val_pred2)
test_pred2=pd.DataFrame(test_pred2)

Combining the meta-features and the validation set, a logistic regression model is built to make predictions on the test set.

df_val=pd.concat([x_val, val_pred1,val_pred2],axis=1)
df_test=pd.concat([x_test, test_pred1,test_pred2],axis=1)

model = LogisticRegression()
model.fit(df_val,y_val)
model.score(df_test,y_test)

Bagging algorithms:

• Bagging meta-estimator

• Random forest

Boosting algorithms:

• AdaBoost

• GBM

• XGBM

• Light GBM

• CatBoost